
雪片曲線論(中沢新一/中央公論社)
「雪片曲線」というのは、何かの文学的な表現なのかと思っていたら、数学用語であるらしい。それは、フラクタルな図形に特有にあらわれる曲線のことで、この本の前半部分は、その不思議な魅力と、自然との近似性について熱く語られている。かなり論文調の堅く難しい文章ではあるけれども、その面白さは充分に伝わってくる。
あちこちの雑誌に掲載された原稿を集めた形になっていて、初出のものは1984年。この25年の間に、フラクタル幾何学という分野でいったいどれほどの進展があったのか、興味が出てきた。
第二部では、1980年代初期の雑多なカルチャーが語られていて、当時「スペースインベーダー」に引き続いて登場した「ゼビウス」についての考察は特に面白い。「茸」の分類不可能性など、様々な分野について、これもまた論文調に分析がまとめられていて、普段聞くことがないような話題ばかりが登場し、著者の幅広い関心が表れている内容だった。
【雪片曲線の作り方】
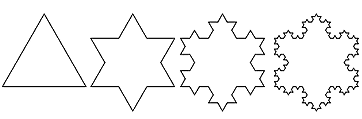
まず正三角形をおく。それに上下を反転させた三角形を重ねると六芒星ができる。その六芒星の一辺それぞれに、1/3の小さい三角突起を作る。さらに、またその一辺に1/3の三角突起を作り、それを数段階繰り返すと、雪片のような結晶模様が出来る。これが「コッホの雪片曲線」である。
【名言】
真言密教などが潜在的にいだいているマンダラの思想を図像表現するには、これまで行われてきたような円や直線を組み合わせて描くユークリッド幾何学的な画法では、まったく不十分なのである。ひとつの空間を埋め尽くすような無数のスケールの渦巻きからなる怪物曲線を生成できる非ユークリッド的なグラフィック技法が必要になる。(p.30)
「雪片曲線」のおもしろさは、そのなかで極端な単純さと極端な複雑さが同居しているところにある。実際、この曲線は実にシンプルで規則的な動作を繰り返すだけで作られる。これに較べれば円の生成の方がはるかに複雑なプロセスをはらんでいるのに、私たちには円が持つ抽象的で単純な性質に「目が眩んで」そのとてつもない複雑さが見えなくなっているのだ。ところが「雪片曲線」の方はその作り方の単純さに反して、信じがたいほどの複雑さを内包している。なぜならその曲線が、無限小の領域に至るまで自己差異化のプロセスに貫かれている、というスタンダードな数学的思考にはとうてい手におえないようなパラドキシカルな性格を持っているためである。(p.74)
レンズ研磨のテクノロジーがもたらしたこの「スケーリング」思想は、バロック的な「自然哲学」にふたつの重要な視点を与えることになったのである。まず「スケーリング」を変化させて、世界を高倍率で捉えていくと、世界はしだいに断片化し、フラクタル化してくる。つまり、粗大な視力にはつるつるでなめらかな「膚」としか見えなかった物質の表面が「スケーリング」を変化させると、でこぼこでギザギザをたくさん持った、少しも均質でない、あばた顔を見せるようになる。無数のすき間やら小穴やらが見えてくるようになるのだ。しかしそのすき間や小穴も、けっして空虚な空間ではなく、さらに「スケーリング」を変化させていくと、より微細な存在の連鎖によって、そこが埋め尽くされているのが見える。(p.90)
『ゼビウス』における物語性の喚起は、「引用」による喚起だ。ゼビウス軍基地の第三エリアを通過するとき、空中にはバキュラと呼ばれる板が多数回転しながら飛来し、プレイヤーが操るソル・バルウをおびやかす。このバキュラが、クラーク=キューブリックによるSF映画『2001年宇宙の旅』に登場する超意識体モノリスを「引用」していることは、ちょっとSFの知識がある人にはすぐ分かる。さらにゼビウス軍基地第七エリアにさしかかると、そこには美しい巨大な「ナスカの地上絵」が現れ、プレイヤーの内部にただちに「宇宙からのメッセージ」をめぐるSF神秘学の薀蓄を喚起するのだ。(p.188)
彼、細野晴臣はこんな風に考えているみたいだ。海の中には大きな目玉を持ったヤリイカの群が、膨大な数で回遊している。ヤリイカの目玉には毎秒数千ビットの情報がはいってくる。しかしヤリイカにはその情報を処理するだけの脳がない。では一体ヤリイカは何のために大きな目玉を開いて回遊しつづけているのか。ヤリイカをとおして地球が「見る」ためである。人間の脳や体だってそれと同じではないか、私たちは大脳をとおして自分がものを考えているように思い込んでいる。けれどそれは子供じみた思いあがりで、実は私たちの大脳をとおして思考しているのは、地球という大きな意識-生命体なのではないか。(p.206)
